Answer:
Option B
Explanation:
Here , $S=S_{1}\cap S_{2} \cap S_{3}$
$S_{1}=\left\{ z\in C:|z|<4\right\}$
$\therefore$ S1 :x2+y2 < 4 ...........(i)
and $S_{2}$ $=\left\{ z\in C :In\left[\frac{z-1+\sqrt{3}i}{1-\sqrt{3}i}\right]>0\right\}$
where $\frac{z-1+i\sqrt{3}}{1-i\sqrt{3}}= \frac{(x-1) +i(y+\sqrt{3})}{1-i\sqrt{3}}$
= $\frac{(x-1)(1+i\sqrt{3})+i(y+\sqrt{3}) (1+i\sqrt{3})}{1+3}$
=$\frac{(x-1)+i\sqrt{3}(x-1)+i(y+\sqrt{3}) -\sqrt{3}(y+\sqrt{3})}{4}$
=$\frac{(x-1-\sqrt{3}y-3)}{4}+\frac{i(\sqrt{3}x+y)}{4}$
$\therefore $ $s_{2}:\sqrt{3}x+y>0$ .......(ii)
$S_{3}=\left\{ z\in C :Re z>0\right\}$
$s_{3}:x>0$ ......(iii)
$s_{3}:x>0$ ......(iii)
Since ,
$S=S_{1}\cap S_{2} \cap S_{3}$
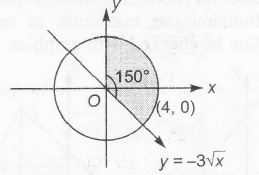
Clearly , the shaded region represents the area of sector
$\therefore$ $S= \frac{1}{2}r^{2}\theta=\frac{1}{2}\times 4^{2}\times\frac{5\pi}{6}=\frac{20\pi}{3}$